Mogan Gh.L., Butilă E.V., Buzdugan I.D. Proiectarea reductoarelor conico-cilindrice. Universitatea Transilvania din Braşov

Anexa.13.1.2 Elemente calcul a arborilor la solicitări variabile (oboseală)

1. Cicluri de solicitare variabilă

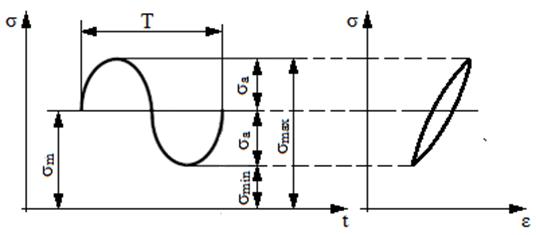
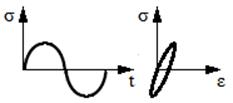
Totalitatea valorilor atinse de tensiunile dintr-un punct al unei structuri în decursul unei perioade de timp determină un ciclu de solicitare care poate fi determinist (valorile sunt funcţii explicite în timp (de obicei, teoretice), fig. a) sau aleator (întâmplător, fig. b, frecvent întâlnit în practică).

Ciclurile de solicitare variabilă deterministe descrise de funcţii periodice (frecvent, sinus) sunt caracterizate de următorii parametri caracteristici: tensiunea maximă, σ_max; tensiunea minimă, σ_min; tensiunea medie,

σ_m = (σ_max + σ_min)/2; amplitudinea ciclului, σ_a = (σ_max - σ_min)/2 (în unele publicaţii notat cu σ_v) ; coeficientul de asimetrie, R = σ_max/σ_min. În tab. a se prezintă cele mai întâlnite cicluri de solicitatre particulare (deterministe) folosite frecvent în proiectare pentru studiul structurilor la solicitări variabile. În cazul structurilor din materiale care pot avea comportări în domeniul plastic sau elasto-plastic pentru ciclurile de solicitare tracţiune-compresiune caracteristica la descărcare este diferită de caracteristica la încărcare şi apare bucla de histeresis (fig. a, caracteristica σ-ε).

a

b

Tab. a

Denumirea ciclului/reprezentare	Caracteristici	Denumirea ciclului/reprezentare	Caracteristici
Oscilant	σm < σa 0 < R < 1	Pulsator	σm = σa R = 0
Alternant	0 < σm < σa -1 < R < 0	Alternant simetric	σm = σa R = -1

2. Cedarea (ruperea) la solicitări variabile

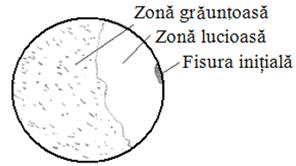
Ruperea la oboseală a unei structuri este cedarea care se produce, puternic localizat, în zonele cu tensiuni şi deformaţii mari (fisură iniţială), consecinţă a unui ansamblu particular de condiţii geometrice, de material şi de sarcini variabile perioade de timp mari (mai mult de 10² …10³ cicluri); tensiunile maxime care apar sunt inferioare rezistenţei la rupere sau chiar limitei de elasticitate a materialului; deformaţiile elastice mari sau chiar plastice se localizează în jurul unor fisuri de suprafaţă sau defecte.

Procesul de rupere la oboseală (fig. e) a unei structuri metalice are un caracter progresiv şi este influenţat de caracteristicile materialului (granulaţia, anizotropia, omogenitatea, fisuri, incluziuni, goluri), formele şi dimensiunile geometrice (concentratori), tehnologiile de fabricaţie (sudare, forjare, turnare, aşchiere, tratamente termice, deformări plastice la rece etc), solicitările şi condiţiile de lucru, temperatura de funcţionare; durata de viaţă (durabilitatea) a unei structuri, de obicei, prin numărul de cicluri până la cedare (rupere).

e

În practică fenomenele de oboseala apar consecinţă a unor solicitări dinamice complexe precum: vibraţii, şocuri repetate, variaţii de temperatură, sarcini variabile periodice şi/sau aleatorii.

Pentru studiul şi calculul la oboseală a structurilor mecanice, deoarece frecvenţa ciclurilor de solicitare nu sunt influenţează semnificativ acet proces, se ia în considerare numărul ciclurilor de solicitare.

Durabilitatea unei structuri este dată de numărul de cicluri de solicitare la care aceasta cedează prin rupere la oboseală.

3. Curba de durabilitate şi rezistenţe (limite) la solicitări variabile (oboseală)

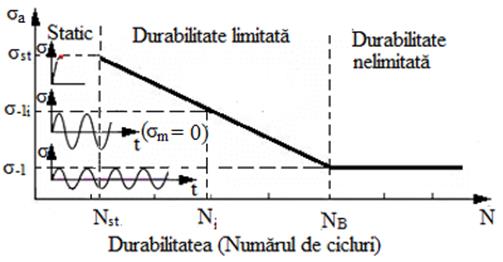
Curba de durabilitate, σ-N (Wohler sau S-N (în literatura în limba engleză) se obţine ca urmare a unor încercări experimentale, pe loturi de epruvete identice (minim 10), încărcate cu sarcini variabile staţionare ciclice cu coeficientul de asimetrie R (frecvent, se foloseşte ciclul alternat simetric cu R = -1, fig. e) şi cu amplitudinea σ_a (diferită pentru fiecare epruvetă, fig. e), pentru care se obţin durabilităţile (numerele de cicluri) N_i la care epruvetele au cedat (se rup). Curba σ-N se obţine prin reprezentarea grafică a perechilor de puncte (σ_a, N_i) într-un sistem de coordonate cu σ_a pe ordonată şi N_i (la scări naturale sau logaritmice, fig. e).

Tensiunea maximă la care epruveta nu se rupe oricât de mult ar fi solicitată, se numeşte limita (rezistenţa) la oboseală (σ_R, σ_-1) corespunzătoare coeficientului de asimetrie al ciclului de solicitare R, respectiv, -1. În practică, pentru oţeluri, se consideră că tensiunea limită (rezistenţa) la oboseală corespunde unei durabilităţi de bază, N_B = 10⁶ … 10⁸ cicluri de solicitare. Practic, σ_-1 = (0,4…0,5) σ_r, pentru oţelurile la încovoiere.

Pentru calculul structurilor mecanice la oboseală se evidenţiază, convenţional, două cazuri de solicitare (fig. e): cu durabilitate limitată (10²…10³ < N < 10⁶…10⁸); cu durabilitate nelimitată (N > 10⁶…10⁸). Pentru calculul de durabilitate nelimitată, rezistenţa la durabilitate corespunzătoare numărului de cicluri de solicitare N_i , σ_-1i > σ_-1.

e - Curba de durabilitate, σ-N (Wohler) în coordonate logaritmice

4. Diagramele rezistenţelor la oboseală (curbele ciclurilor limită) şi schematizări (simplificari) ale acestora

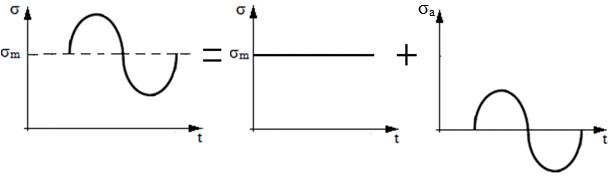
În general, valorile caracteristice de materialse obţin prin încercări la cicluri alternant simetrice R = -1 pentru care tensiunea medie σ_m = 0. Un ciclu de solicitare real aproximabil cu un ciclu alternant cu R = [-1, 1]) se poate considera ca ciclu alternat simetric de amplitudine σ_a (uneori notat σ_v) cu suprapus peste o solicitare constantă egală cu tensiunea medie σ_m (fig. f).

f – Descompunerea ciclului oscilant

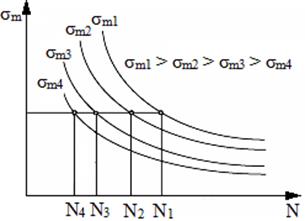
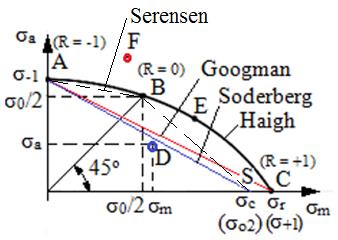
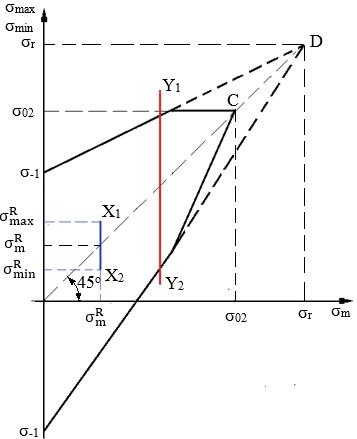
Experimental s-a evidenţiat că în cazul durabilităţilor mari creşterea tensiunilor medii scurtează viaţa structurii (piesei), fig. g.

Ciclul de solicitare cu coeficientul de asimetrie R (cu tensiuni medii σ_m ≠ 0) şi cu tensiunea maximă σ_max egală cu rezistenţa la oboseală a materialului (σ_-1) se numeşte ciclu limită. Efectul tensiunii medii se cuantifică în diagrama rezistenţelor la oboseală sau curba ciclurilor limită (locul geometric al punctelor corespunzătoare ciclurilor limită) care evidenţiază variaţia rezistenţei la oboseală cu coeficientul de asimetrie, -1 < R < 1 (Haigh, fig. h). În practică aceste diagrame permit determinarea rezistenţelor la oboseală în funcţie de coeficienţii de asimetrie R (sau de σ_m şi σ_a).

Diagramele de tip High evidenţiază dependenţa amplitudinii ciclului de solicitare σ_a în funcţie de tensiunea medie, σ_m. În aceste diagrame fiecare punct este asociat unui ciclu de solicitare R dintre care în fig. h sunt marcate: A – alternat simetric (R = -1), B – pulsator (R = 0), C – static (R = +1), E – alternant/oscilant (-1 < R < 1). În cazul în care ciclul de solicitare real corespunde punctului D din interiorul curbei AC, structura rezistă la oboseală, iar dacă corespunde punctului F din exteriorul acesteia, structura cedează prin rupere la oboseală. Obţinerea unei diagrame High în formă completă este aproape imposibilă, deoarece necesită încercări la oboseală pentru foarte multe cicluri (teoretic infinit) cu coeficienţi de asimetrie în domeniul [-1, 1] şi, ca urmare, pentru scopuri practice s-au propus schematizări (simplificări) ale acetor diagrame. În practica de proiectare a structurilor mecanice se folosesc frecvent simplificările liniare Goodman (pentru materiale fragile) şi Soderberg (pentru materiele tenace) care înlocuiesc curba AC cu dreapta AC (punctul C corespunnde tensiunii de rupere statică σ_r) şi, respectiv, dreapta AS (punctul S corespunde tensiunii limită de curgere σ_c).

Diagramele de tip Smith evidenţiază dependeţe ale tensiunilor maxime şi minime, σ_max respectiv σ_min în funcţie de tensiunea medie, σ_m (fig. i). În această diagramă apar două contururi ale ciclurilor limită, unul pentru tensiunile maxime şi cealalt pentru tensiunile minime. Cele două contururi se întâlnesc în punctul C corespunzător limitei (rezistenţei) la curgere, pentru oţelurile tenace, şi în D, pentru materialele casante. Ciclurile asociate punctelor din interiorul celor două contururi (de ex. X₁X₂) asigură necedarea prin oboseală iar în cele asociate punctelor din exteriorul acestora (de ex. Y₁Y₂) apare ruperea prin oboseală. Punctele de pe cele două contururi sunt asociate ciclurilor limită particulare (alternant simetric, pulsator, static). Şi în cazul diagramelor Smith pentru calculul practic la oboseală s-au adoptat schematizări (simplificări), de obicei, având la bază valori cunoscute despre material (de ex. σ_c sau σ_r)

g – Curbe de oboseală pentru diferite tensiuni medii h – Diagrame High

i – Diagrame Smith